Teoria da Proporcionalidade: a famosa “Regra de Três”

Introdução:
A teoria da proporcionalidade é um importante conceito matemático que desempenha um papel fundamental no estudo das relações entre quantidades. Ela é bastante abordada no ensino de matemática para alunos, em especial, do 7 ano. Pois, oferece uma base sólida para compreender e resolver uma variedade de problemas envolvendo proporções. Portanto, neste texto iremos explorar o que é a teoria da proporcionalidade, como ela funciona e sua importância no mundo real.
1. O que é proporção?
Uma proporção é uma igualdade entre duas razões. Por exemplo, se tivermos duas quantidades A e B, podemos dizer que elas estão em proporção se a razão entre A e B for igual à razão entre C e D. Isso pode ser expresso como:
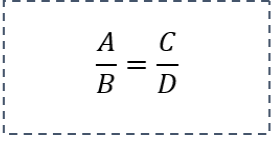
Quando temos uma proporção, podemos usar regras matemáticas para encontrar valores desconhecidos. Isso é especialmente útil em situações onde conhecemos parte da informação e queremos descobrir outra parte: https://mundodamatematica.com.br/wp-admin/post.php?post=308&action=edit
2. Exemplos de proporcionalidade:
Um exemplo clássico de proporcionalidade é o cálculo de distâncias em mapas. Se sabemos que 1 centímetro no mapa representa 10 quilômetros na realidade, podemos usar uma proporção para encontrar a distância real entre dois pontos no mapa.
Outro exemplo é o cálculo de preços em supermercados. Se um produto custa $2.50 por 500 gramas, podemos usar proporções para descobrir quanto custaria 1 quilo desse produto.
3. Regra de três:
A regra de três é uma ferramenta fundamental na teoria da proporcionalidade. Ela permite que você encontre um valor desconhecido quando conhecemos três valores em proporção. Por exemplo, se sabemos que 2 litros de um suco custam $4 e queremos saber quanto custam 3 litros, podemos usar a regra de três para encontrar a resposta.
Conclusão:
Portanto, a teoria da proporcionalidade desempenha um papel crucial em nossa vida cotidiana, ajudando-nos a resolver uma variedade de problemas práticos. Ela fornece uma base sólida para o desenvolvimento de habilidades matemáticas e a capacidade de tomar decisões informadas em diversas situações. À medida que avançamos no estudo da matemática, a compreensão da proporcionalidade nos permite lidar com desafios cada vez mais complexos, preparando-nos para enfrentar o mundo com confiança e habilidade.




0 Comentários