Teorema de Euler

Introdução:
O Teorema de Euler para poliedros é uma das descobertas fundamentais da matemática, estabelecendo uma relação profunda entre as faces, as arestas e os vértices de um poliedro convexo. Formulado por Leonhard Euler no século XVIII, esse teorema oferece uma visão elegante da estrutura dos poliedros e tem aplicações em diversas áreas da matemática e da engenharia. Neste texto, exploraremos o Teorema de Euler para poliedros, apresentaremos um desafio e uma matemática no cotidiano.
Formulação do Teorema de Euler
O Teorema de Euler estabelece uma relação crucial entre os vértices (V), as arestas (A) e as faces (F) de um poliedro convexo. De acordo com este teorema, a soma dos vértices, arestas e faces de um poliedro é sempre constante e igual a dois mais o número de faces menos o número de arestas. Em termos matemáticos, a fórmula pode ser expressa como:
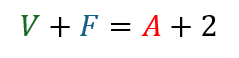
Essa fórmula simples, mas profunda, revela uma conexão intrínseca entre os diferentes componentes de um poliedro, oferecendo uma maneira elegante de analisar sua estrutura.
Exemplos
- Considere um poliedro convexo com 4 vértices, 6 arestas e faces? Aplicando a fórmula de Euler, temos:
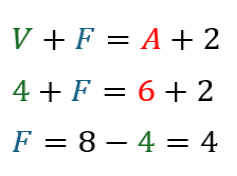
- Considere agora, outro poliedro convexo com 8 vértices, arestas? e 6 faces. Aplicando a fórmula de Euler, temos:
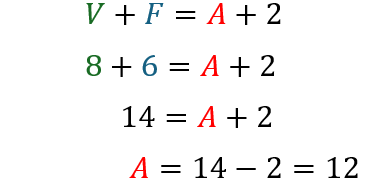
Mais uma vez, o resultado está em conformidade, reforçando sua aplicabilidade em uma variedade de contextos.
Implicações e Aplicações
O Teorema de Euler tem implicações profundas em várias áreas da matemática e da engenharia. Por exemplo, é fundamental na topologia, onde é utilizado para estudar as características dos espaços tridimensionais. Além disso, o teorema é frequentemente aplicado na computação gráfica para otimizar algoritmos de renderização de objetos tridimensionais.
Conclusão:
O Teorema de Euler para poliedros é uma contribuição significativa para a teoria dos poliedros e tem vastas aplicações em diferentes campos da matemática e da engenharia. Ao longo deste texto, exploramos o teorema, apresentando sua formulação, exemplos ilustrativos e implicações práticas. Ele continua a ser uma ferramenta indispensável para os matemáticos e cientistas, destacando a elegância e a profundidade que podem ser encontradas na teoria matemática.
Matemática no cotidiano: Matemática e Finanças
A matemática desempenha um papel fundamental em nossas vidas cotidianas, especialmente quando se trata de finanças. Desde as compras diárias até o planejamento de investimentos de longo prazo, a matemática é essencial para tomar decisões financeiras informadas e eficazes.
Orçamento Pessoal e Despesas Diárias
A matemática nos ajuda a administrar nosso dinheiro de maneira eficiente, principalmente por meio do planejamento de orçamento pessoal. Ao calcular nossos rendimentos e despesas, podemos determinar quanto podemos gastar em diferentes categorias, como moradia, alimentação, transporte e entretenimento. A habilidade de realizar cálculos simples, como adição, subtração, multiplicação e divisão, é crucial para acompanhar nossas despesas diárias e garantir que permaneçamos dentro do nosso orçamento.
Juros e Empréstimos
Entender conceitos matemáticos como juros simples e compostos é essencial ao lidar com empréstimos, hipotecas e cartões de crédito. Ao calcular os juros sobre um empréstimo ou investimento, podemos tomar decisões informadas sobre quais opções são mais vantajosas a longo prazo. Compreender a matemática por trás dos juros também nos ajuda a evitar dívidas excessivas e a economizar dinheiro ao longo do tempo.
Investimentos e Planejamento de Aposentadoria
A matemática desempenha um papel crucial no planejamento financeiro de longo prazo, especialmente quando se trata de investimentos e planejamento de aposentadoria. Ao calcular taxas de retorno, avaliar o risco e projetar crescimento futuro, podemos criar estratégias de investimento que nos ajudem a alcançar nossos objetivos financeiros. Ferramentas matemáticas como cálculo de juros compostos, valor presente líquido (VPL) e taxa interna de retorno (TIR) nos auxiliam na tomada de decisões inteligentes sobre onde investir nosso dinheiro para garantir uma aposentadoria confortável.
Desafio do dia: Juros compostos
Suponha que você tenha investido R$ 5.000,00 em uma conta de investimento que rende juros compostos a uma taxa de 8% ao ano. Quanto dinheiro você terá após 3 anos?
Dados:
- Capital inicial (C): R$ 5.000,00
- Taxa de juros ao ano (i): 8% ou 0,08
- Período de tempo (n): 3 anos
Fórmula para Juros Compostos: A=C×(1+i)n





0 Comentários