Sistemas de equações

Introdução:

Os sistemas de equações são uma parte fundamental do currículo de matemática no ensino médio. Eles são uma ferramenta poderosa para resolver problemas do mundo real que envolvem múltiplas incógnitas e relações entre elas. Neste texto, exploraremos os conceitos básicos dos sistemas de equações, suas diferentes formas de representação, métodos de resolução e aplicações práticas.

O que são sistemas de equações?

Um sistema de equações consiste em um conjunto de duas ou mais equações que compartilham as mesmas incógnitas. As soluções do sistema são os valores das incógnitas que satisfazem todas as equações simultaneamente. Por exemplo, considere o seguinte sistema de equações lineares:

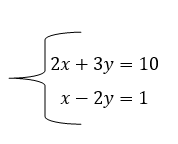
Neste sistema, temos duas equações (a primeira equação e a segunda equação) e duas incógnitas (x e y).

Formas de representação de sistemas de equações:

Os sistemas de equações podem ser representados de diferentes formas, dependendo da situação e do contexto do problema. As formas mais comuns incluem:

• Forma padrão: Nesta forma, as equações são escritas uma abaixo da outra, separadas por uma linha horizontal. Por exemplo, o sistema mencionado anteriormente está na forma padrão.
• Forma matricial: Os coeficientes das equações e os termos independentes são organizados em matrizes. Por exemplo, o sistema anterior pode ser representado na forma matricial como:

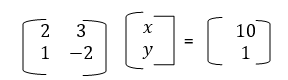
• Forma vetorial: Nesta forma, as equações são escritas em termos de vetores e produtos internos. Por exemplo, o sistema pode ser representado na forma vetorial como:

⟨2,3⟩⋅⟨x,y⟩=10

⟨1,−2⟩⋅⟨x,y⟩=1

Métodos de resolução de sistemas de equações:

Existem várias maneiras de resolver sistemas de equações, sendo os métodos mais comuns:

1. Método de substituição: Neste método, uma das equações é resolvida para uma das incógnitas em termos da outra e então essa expressão é substituída na outra equação. Por exemplo, dado o sistema:

Podemos resolver a segunda equação para x=2y+1 e substituir essa expressão na primeira equação, resultando em uma equação com apenas uma incógnita, y.

2. Método de eliminação: Neste método, as equações são manipuladas de modo que, quando somadas ou subtraídas, uma das incógnitas é eliminada. Este método é particularmente útil quando os coeficientes de uma das incógnitas são opostos. Continuando com o exemplo anterior, podemos multiplicar a segunda equação por 2 e adicioná-la à primeira equação para eliminar x.
3. Método gráfico: Neste método, as equações são representadas graficamente em um plano cartesiano e as soluções comuns são determinadas pela interseção dos gráficos das equações.

Aplicações práticas dos sistemas de equações:

Os sistemas de equações têm numerosas aplicações práticas em diversas áreas, incluindo economia, engenharia, física e ciências sociais. Por exemplo, eles podem ser usados para modelar situações de mistura, problemas de otimização, análise de circuitos elétricos e muito mais.

Conclusão:

Os sistemas de equações são uma ferramenta poderosa para resolver problemas do mundo real que envolvem múltiplas incógnitas e relações entre elas. Eles são representados de várias formas e podem ser resolvidos usando uma variedade de métodos. Dominar esses conceitos é fundamental para desenvolver habilidades matemáticas e para aplicar a matemática em situações da vida real.

Tags: Álgebra | BNCC | EF08MA08 | Matemática | SISTEMA DE EQUAÇÃO | SISTEMAS