Matemática financeira: juros compostos e investimentos

Introdução:
A matemática financeira é uma ferramenta essencial para entender e gerenciar recursos financeiros de forma eficiente. Nesse contexto, eles desempenham um papel fundamental, pois representam o ganho ou custo gerado por investimentos ou empréstimos ao longo do tempo. Este texto abordará a dinâmica dos juros compostos e sua aplicação em investimentos, fornecendo exemplos elucidativos para uma compreensão mais clara e também, apresenta uma curiosidade e um desafio do dia.
Conceito de Juros Compostos
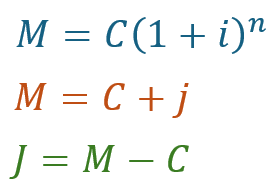
C é o capital inicial (ou principal);
i é a taxa de juros (em decimal);
n é o número de vezes que os juros são compostos por ano;
J é o tempo em anos.
Eles, referem-se ao cálculo sobre o capital inicial somado aos acumulados em períodos anteriores. Diferentemente dos simples, onde estes são calculados apenas sobre o capital inicial, nos compostos, os rendimentos são reinvestidos, gerando um crescimento exponencial do capital ao longo do tempo.
- Exemplo de Investimento com Juros Compostos
Suponha que um investidor aplique R$ 10.000,00 em uma instituição financeira que oferece uma taxa de juros compostos de 8% ao ano. Após o primeiro ano, o investimento renderá R$ 800,00 em juros (10.000 * 0,08). No entanto, ao final do segundo ano, os juros serão calculados sobre R$ 10.800,00 (capital inicial + juros do primeiro ano), resultando em R$ 864,00 de juros (10.800 * 0,08). Esse processo se repete a cada período de capitalização, aumentando progressivamente o retorno do investimento.
Comparação entre Juros Compostos e Juros Simples
Link: https://mundodamatematica.com.br/rascunho-automatico-/
Para ilustrar a diferença entre juros compostos e juros simples, consideremos o mesmo exemplo anterior, porém com o simples. Com uma taxa de 8% ao ano, o investidor teria um retorno fixo de R$ 800,00 a cada ano, independentemente do período de investimento. Portanto, ao longo do tempo, a diferença entre os retornos de simples e compostos se torna significativa, destacando a vantagem dos compostos na geração de riqueza a longo prazo.
Aplicações Práticas dos Juros Compostos
Eles, são amplamente utilizados em diversas áreas financeiras, incluindo investimentos em renda fixa e variável, empréstimos, financiamentos imobiliários, entre outros. Por exemplo, ao investir em fundos de investimento ou na bolsa de valores, os investidores se beneficiam do poder deles para aumentar seus ganhos ao longo do tempo.
Conclusão:
Em suma, a compreensão dos juros compostos é essencial para tomar decisões financeiras informadas e maximizar os retornos dos investimentos. Ao entende-los funcionam e sua aplicação em diferentes contextos, os investidores podem potencializar seus ganhos e alcançar seus objetivos financeiros de longo prazo. Portanto, a matemática financeira, com foco neles, é uma ferramenta poderosa para quem busca otimizar suas finanças pessoais ou empresariais.
Curiosidade: Matemática em técnicas de animação e efeitos especiais
- A matemática desempenha um papel fundamental nas técnicas de animação e efeitos especiais, impulsionando a criação de mundos digitais impressionantes e realistas. Desde a geração de movimentos fluidos até a simulação de fenômenos físicos, os princípios matemáticos são essenciais para garantir a autenticidade e a qualidade visual nas produções cinematográficas modernas.
- Um dos aspectos mais importantes é a aplicação de geometria e álgebra na modelagem 3D. Os objetos e personagens digitais são construídos usando formas geométricas básicas, como polígonos, que são manipulados e transformados por meio de equações matemáticas. Além disso, a trigonometria é frequentemente utilizada para calcular ângulos de rotação e direção de movimento, garantindo animações suaves e realistas.
- Outro aspecto crucial é a física computacional, que utiliza conceitos matemáticos para simular o comportamento de elementos naturais, como água, fogo e partículas. Equações diferenciais são empregadas para modelar o movimento e a interação desses elementos, permitindo a criação de efeitos especiais convincentes.
Desafio do dia: Calcule o retorno de um investimento com juros compostos
1 – Suponha que você investiu R$ 5.000,00 a uma taxa de juros compostos de 6% ao ano. Quanto dinheiro você terá após 3 anos?




0 Comentários