Função Quadrática: Uma Exploração Profunda

Introdução:
A função quadrática, também conhecida como função do segundo grau, desempenha um papel fundamental na matemática e em muitas áreas da ciência e engenharia. Neste texto, iremos explorar a função quadrática em detalhes, desde sua definição até suas aplicações práticas. Abordaremos tópicos como a forma geral, seu gráfico, suas raízes, o vértice da parábola e algumas aplicações em situações do mundo real.
Sobre a Função Quadrática:
https://mundodamatematica.com.br/rascunho-automatico-funcao/
A função quadrática é uma função polinomial do segundo grau, geralmente expressa na forma:
Onde a, b, e c são constantes, e a não pode ser igual a zero, uma vez que isso resultaria em uma função linear. Ela é chamada assim devido ao termo ax2, que é o termo quadrático.
O Gráfico da Função Quadrática:
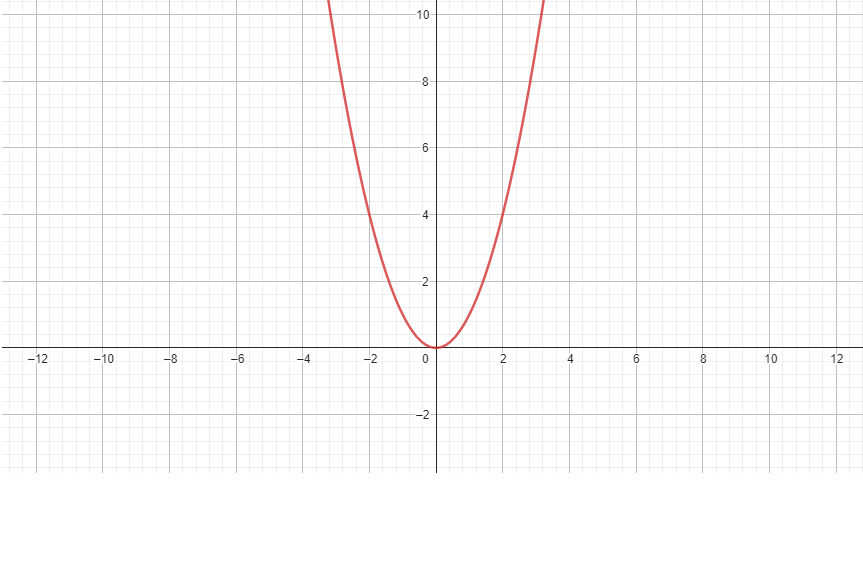
Um dos aspectos mais importantes é seu gráfico, que é uma parábola. A concavidade da parábola (se ela se abre para cima ou para baixo) é determinada pelo coeficiente a. Se for positivo, a parábola se abrirá para cima e, se for negativo, a parábola se abrirá para baixo.
Para visualizar melhor o gráfico da função, podemos usar a fórmula do vértice:
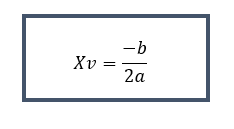
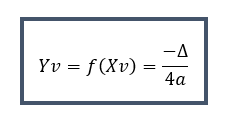
Onde Δ é o discriminante, dado por Δ=b2−4ac. O ponto (xv,yv) é o vértice da parábola, que é o ponto de mínimo ou máximo, dependendo da concavidade da parábola.
Raízes da Função Quadrática:
As raízes de uma função quadrática são os valores de x para os quais f(x)=0. Para encontrar as raízes, podemos usar a fórmula quadrática:
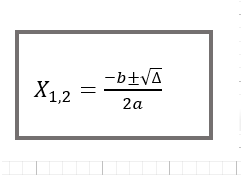
Aqui, Δ é o discriminante, como mencionado anteriormente. Ela pode ter duas raízes reais distintas se Δ>0, uma raiz real (raiz dupla) se Δ=0, ou nenhuma raiz real se Δ<0.
O Vértice da Parábola:
O vértice da parábola, como mencionado anteriormente, é o ponto de mínimo ou máximo da função. Se a parábola se abrir para cima (a>0), o vértice é o ponto mais baixo da parábola, e se a parábola se abrir para baixo (a<0), o vértice é o ponto mais alto. O vértice da parábola é encontrado nas coordenadas (xv,yv), onde xv é dado pela fórmula do vértice e yv é o valor de f(xv).
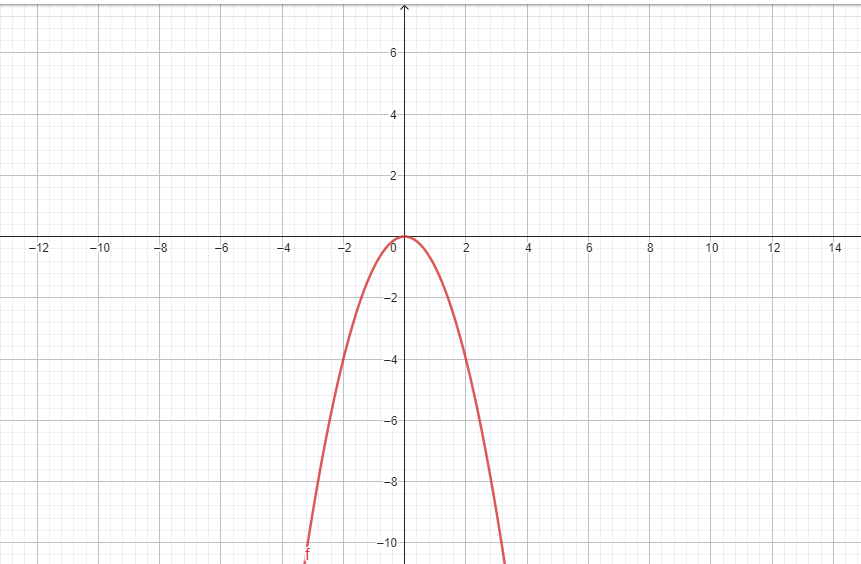
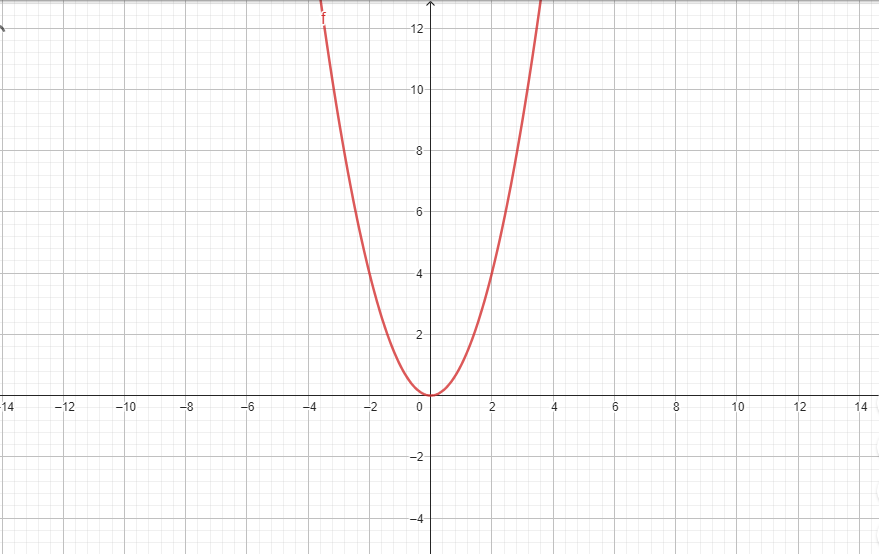
https://www.geogebra.org/calculator
Aplicações da Função Quadrática:
A função quadrática é amplamente utilizada em diversas áreas. Aqui estão algumas aplicações práticas:
1. Física: Usa-se para descrever o movimento de um objeto sob a influência da gravidade. A equação da trajetória de um objeto em queda livre é um bom exemplo.
2. Engenharia: Usa-se funções quadráticas para projetar estruturas, calcular a forma de arcos, parábolas e muito mais. Essas funções ajudam a otimizar o design de diversas estruturas.
3. Economia: Usa-se em análises de custos, receitas e lucros de empresas. Ela ajuda a determinar o ponto de equilíbrio onde as receitas e os custos são iguais.
Conclusão:
Em resumo, a função quadrática é um conceito matemático fundamental com diversas aplicações no mundo real. Ela descreve a relação entre uma variável independente x e uma variável dependente y por meio de uma equação polinomial do segundo grau. Com a compreensão da forma geral, seu gráfico, raízes e vértice, podemos utilizá-la para resolver problemas complexos em diversas áreas, desde a física até a economia. Dominá-la é essencial para aprofundar nosso conhecimento em matemática e aplicá-la de maneira eficaz em nossa vida cotidiana e em carreiras técnicas e científicas.




0 Comentários