função logarítmica

Introdução:

No ensino médio, os alunos são apresentados a uma variedade de conceitos matemáticos complexos e poderosos, e um deles é a função logarítmica. Embora possa parecer intimidante à primeira vista, as funções logarítmicas desempenham um papel fundamental em várias áreas da matemática e da ciência. Neste texto, vamos explorar o universo das funções logarítmicas, desde sua definição básica até suas aplicações práticas. Prepare-se para uma jornada empolgante rumo ao entendimento dessa importante função matemática.

O que são Funções Logarítmicas?

As funções logarítmicas são uma classe de funções matemáticas que desempenham um papel crucial na modelagem e resolução de uma variedade de problemas em matemática, ciências naturais e engenharia. Elas são frequentemente usadas para descrever crescimento exponencial e são o inverso das funções exponenciais. A forma geral de uma função logarítmica é dada por:

onde:

• f(x) representa a variável dependente.
• x representa o Logaritmando.
• a representa à base.

Importante lembrar que, se um logaritmo “c” na base “a” igual ao expoente “x”, deve-se elevar à base “a” fazendo com que:

Exemplos:

• Log₅ 25 = x implica que 5^x = 25.
• Log₂ 4 = x implica que 2^x = 4.

Propriedades das Funções Logarítmicas:

As funções logarítmicas possuem várias propriedades importantes que facilitam sua manipulação e solução de problemas. Algumas dessas propriedades incluem:

Produto:

• log_a​(x.y)=log_a​(x)+log_a​(y)

Quociente:

• log_a​(x/y)=log_a​(x)−log_a​(y)

Expoente:

• log_a(xⁿ)=n⋅log_a​ x

Do numero 1:

• log_a1 = 0

Exemplos de Aplicações:

Modelagem de Crescimento Exponencial

As funções logarítmicas, são geralmente usadas para modelar fenômenos de crescimento exponencial como o crescimento populacional, o decaimento radioativo e o crescimento de investimentos financeiros. Por exemplo, se tivermos uma população inicial P₀​ e uma taxa de crescimento anual de r, podemos usar a função logarítmica para calcular o tempo necessário para que a população atinja um determinado valor P.

Engenharia e Ciências Naturais

As funções logarítmicas também desempenham um papel fundamental na resolução de problemas em engenharia e ciências naturais. Pois, na física, para encontrar o pH de uma solução ácida, basta calcular a função logarítmica.

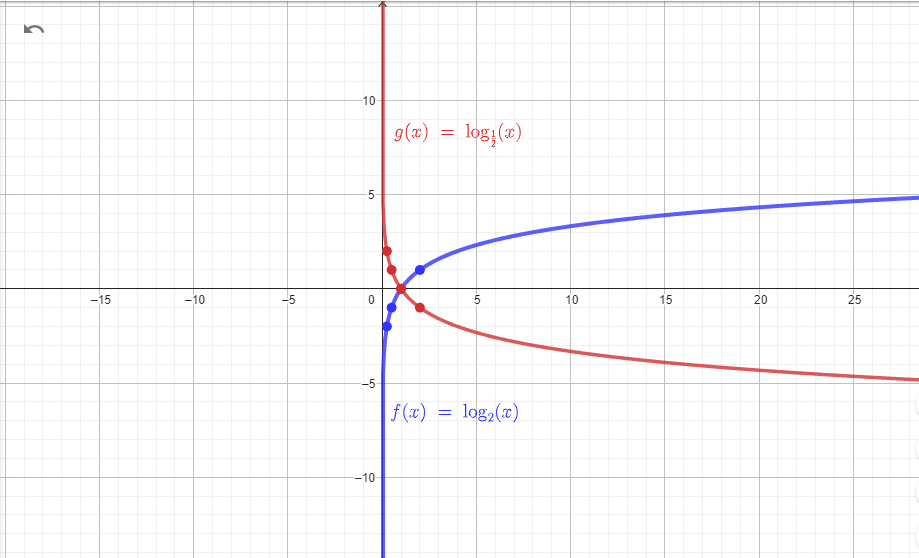
Gráficos de Funções Logarítmicas:

Os gráficos das funções logarítmicas têm características distintas. Eles são geralmente crescentes, mas com uma taxa de crescimento que diminui à medida que x aumenta. O eixo das x é um assíntota vertical, e o eixo das y é o eixo horizontal. Os gráficos também passam pela origem, ou seja, log_a(1)=0.

Conclusão:

As funções logarítmicas são uma ferramenta poderosa e versátil em matemática e ciências. Elas permitem a modelagem de fenômenos de crescimento exponencial, resolvem equações complexas e têm aplicações em diversas áreas da engenharia e das ciências naturais. Os alunos do ensino médio podem dominar essa importante função matemática, portanto, mergulhem de cabeça no mundo das funções logarítmicas, pois elas desempenham um papel fundamental no nosso entendimento do mundo ao nosso redor e na resolução de problemas complexos.

Tags: (EM13MAT305) | BNCC | ensino médio | FUNÇÕES | logarítmo | Matemática | números