Explorando a potência da função exponencial

A função exponencial é um tópico fundamental no currículo de matemática. Ela desempenha um papel crucial na compreensão de fenômenos naturais, no crescimento de populações, na modelagem de investimentos financeiros e em várias outras aplicações. Neste texto, exploraremos o conteúdo, abordando suas propriedades e exemplos práticos.
Conceito de Função Exponencial: https://mundodamatematica.com.br/rascunho-automatico-funcao/
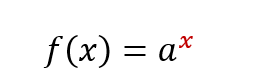
Uma função exponencial é uma função matemática, onde “a” é uma constante positiva chamada de base, e “x” é a variável independente. A base “a” deve ser maior que zero e diferente de um para que seja verdadeiramente exponencial. A variável “x” representa o expoente, e o valor da função f(x) é calculado elevando a base a à potência x.
Propriedades:
As funções exponenciais possuem várias propriedades importantes, incluindo:
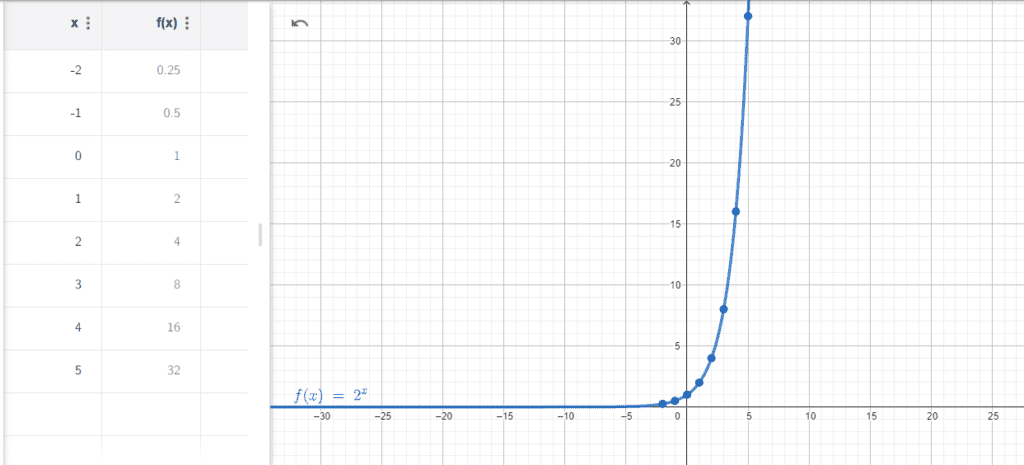
- Crescimento Exponencial: Quando a base “a” é maior que 1, a função exponencial cresce rapidamente à medida que “x” aumenta. Quanto maior for o valor de x, maior será o valor da função f(x).
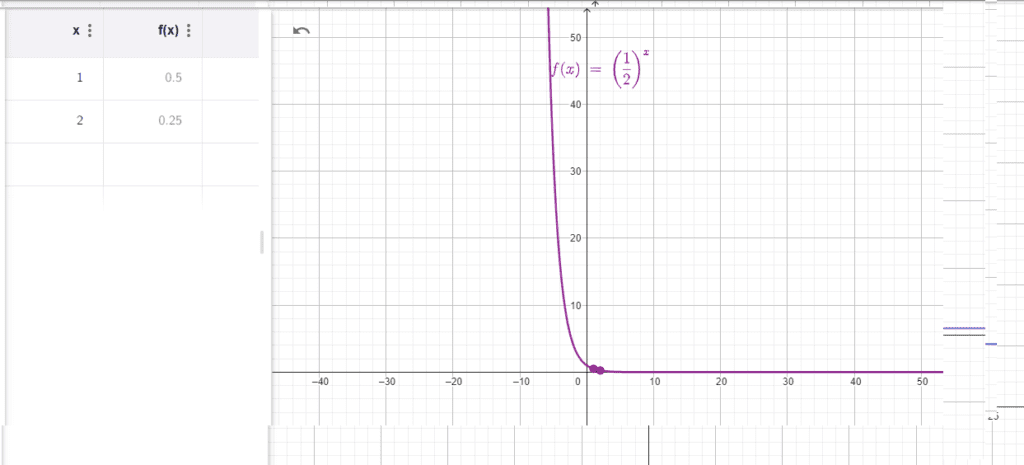
- Decaimento Exponencial: Quando a base “a” está entre 0 e 1, a função exponencial decresce à medida que x aumenta. Quanto maior for o valor de “x”, menor será o valor da função f(x).
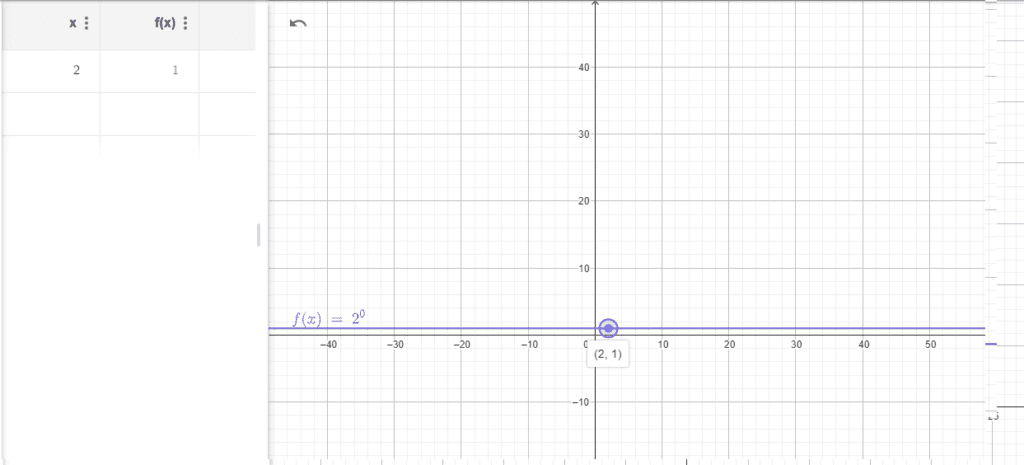
- Propriedade do Zero: Para qualquer base a, a0 = 1. Isso significa que a função exponencial sempre possui um valor de 1 quando x é igual a zero.
Exemplos:
A seguir, apresentamos alguns exemplos de função exponencial para ilustrar essas propriedades:
Exemplo 1: f(x)=2x
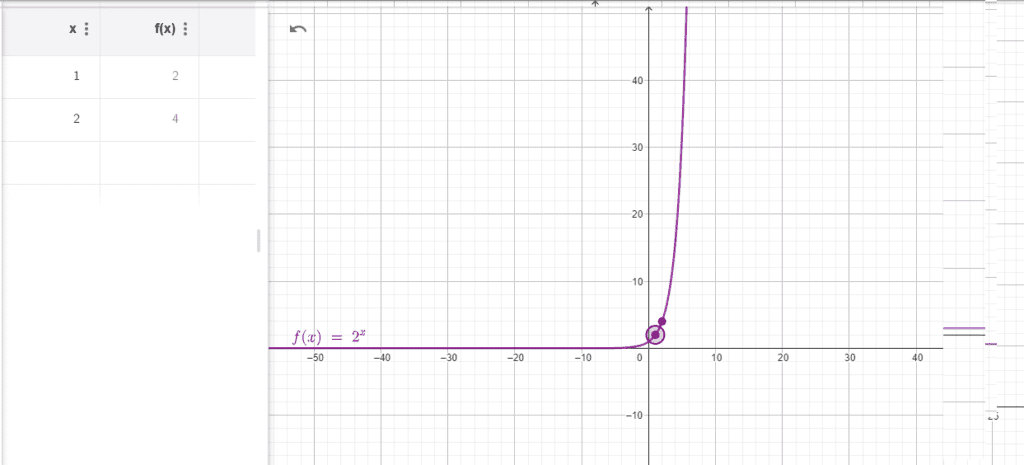
Neste caso, a base é a=2, o que significa que a função cresce exponencialmente à medida que x aumenta. Se calculássemos f(1), obteríamos 21=2, e se calculássemos f(2), obteríamos 22=4. O crescimento é notável, já que f(2) é o dobro de f(1), e assim por diante.
Exemplo 2: g(x)=0.5x
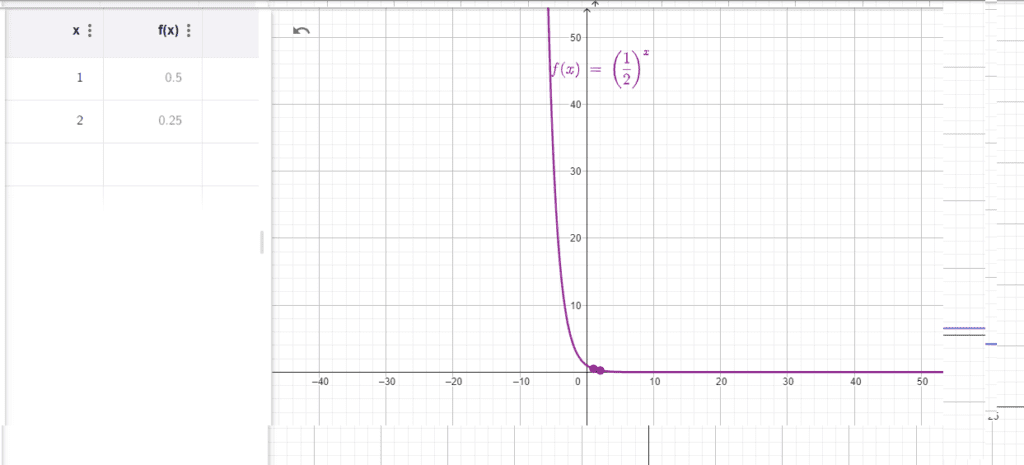
Neste exemplo, a base é a=0.5, o que indica um decaimento exponencial. Quando calculamos g(1), obtemos 0.51=0.5, e g(2) resulta em 0.52=0.25. A função diminui rapidamente à medida que x aumenta.
Aplicações da Função Exponencial:
A função exponencial é amplamente utilizada em diversas áreas da matemática e da ciência. Aqui estão algumas aplicações práticas:
- Crescimento Populacional: É frequentemente usada para modelar o crescimento de populações, como a reprodução de organismos ou o aumento da população humana ao longo do tempo. Por exemplo, se soubermos a taxa de crescimento anual de uma população, podemos usa- lá para prever o tamanho da população no futuro.
- Investimentos Financeiros: Ela também é aplicada na área de finanças para modelar o crescimento de investimentos ao longo do tempo. Quando você investe dinheiro com juros compostos, seu investimento cresce exponencialmente.
- Decaimento Radioativo: É usada para descrever o decaimento radioativo de elementos. A taxa de decaimento é constante, e a quantidade de material radioativo restante diminui exponencialmente ao longo do tempo.
Conclusão:
A função exponencial é um conceito essencial no primeiro ano do ensino médio, oferecendo uma base sólida para compreender o crescimento e o decaimento exponenciais. Ela desempenha um papel importante em várias áreas da matemática e da ciência, permitindo-nos modelar fenômenos naturais e tomar decisões informadas em finanças e outros campos. Com uma compreensão sólida, os alunos estarão preparados para explorar tópicos mais avançados em matemática e ciências em anos subsequentes.




0 Comentários