Função: A chave fundamental nos avanços da matemática

Introdução:
As funções são ferramentas matemáticas poderosas que descrevem as relações entre variáveis e são amplamente aplicáveis em várias áreas da matemática e da ciência. Neste conteúdo, exploraremos o conteúdo de Função – apresentando conceitos, exemplos e sua importância.
O que é uma função?
Uma função é uma relação matemática que associa cada elemento de um conjunto de entrada (domínio) a um único elemento em um conjunto de saída (contradomínio). Em outras palavras, uma função atribui a cada valor de entrada um valor correspondente de saída, sem ambiguidade. Isso significa que, para cada valor de x no domínio, há um único valor de y no contradomínio.
Representação de funções:
As funções podem ser representadas de várias maneiras. A representação mais comum é por meio de equações.
- Por exemplo, a função f(x) = 2x é uma função linear que dobra o valor de x. Para cada valor de x que inserimos, obtemos um valor correspondente de y, multiplicando x por 2. Isso pode ser representado graficamente como uma reta que passa pela origem, com inclinação de 2.
Domínio e contradomínio:
O domínio de uma função é o conjunto de todos os valores possíveis de entrada (x) para os quais ela está definida. O contradomínio, por outro lado, é o conjunto de todos os valores possíveis de saída (y) que a função pode assumir. Nem todos os valores de y no contradomínio precisam ser obtidos, mas cada valor em x deve ter uma correspondência única em y.
Exemplos de funções:
Vamos explorar alguns exemplos de funções simples:
- Função Linear: f(x) = 2x
- Domínio: Todos os números reais
- Contradomínio: Todos os números reais
- Exemplo de mapeamento: Se x = 3, então f(3) = 2 * 3 = 6.
- Função Quadrática: f(x) = x^2
- Domínio: Todos os números reais
- Contradomínio: Todos os números reais não negativos
- Exemplo de mapeamento: Se x = -2, então f(-2) = (-2)^2 = 4.
- Função Raiz Quadrada: f(x) = √x
- Domínio: Números reais não negativos (x ≥ 0)
- Contradomínio: Números reais não negativos (f(x) ≥ 0)
- Exemplo de mapeamento: Se x = 9, então f(9) = √9 = 3.
Gráfico de Funções:
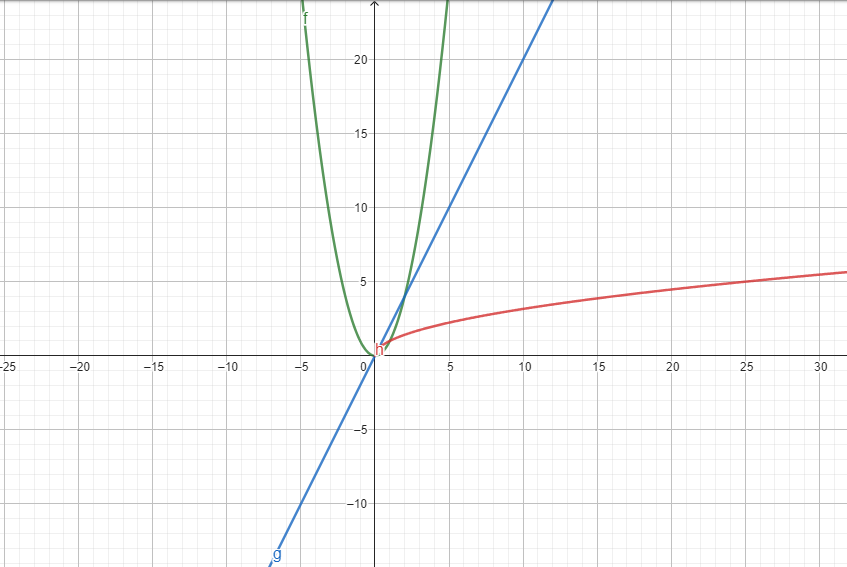
Uma maneira comum de visualizar funções é por meio de gráficos. Cada ponto (x, y) no gráfico representa uma entrada x e a saída correspondente y da função. O gráfico de uma função linear é uma reta, enquanto o de uma função quadrática é uma parábola. O gráfico da função raiz quadrada é uma curva que começa em (0, 0) e cresce lentamente à medida que x aumenta.
Conclusão:
As funções são um conceito fundamental na matemática que desempenham um papel crucial em muitos campos da ciência e engenharia. Elas representam relações matemáticas entre variáveis e podem ser expressas de várias maneiras, incluindo equações e gráficos.
Entender os conceitos de domínio, contradomínio, representação gráfica e exemplos de funções é essencial para o sucesso no estudo da matemática e sua aplicação em várias áreas. À medida que os alunos progridem em seus estudos, eles encontrarão funções mais complexas e aprenderão a aplicá-las em contextos práticos, tornando esse conceito uma base sólida para sua educação matemática futura. Portanto, o estudo das funções no primeiro ano do ensino médio é uma etapa importante na jornada de aprendizado dos estudantes.




0 Comentários