Matemática: A beleza das equações

Introdução:
As equações matemáticas são como poesias abstratas, capturando a essência da ordem e da beleza subjacentes ao universo. Algumas dessas equações transcendem sua utilidade prática, alcançando um status quase mítico entre os matemáticos e entusiastas. Neste texto, exploraremos algumas das mais belas equações matemáticas, revelando sua elegância e profundidade e também, apresentaremos uma curiosidade e um desafio do dia.
Equação de Euler: A beleza da harmonia

A primeira equação que merece destaque é a famosa identidade de Euler. Esta equação combina cinco dos números mais importantes da matemática: e, a base dos logaritmos naturais; i, a unidade imaginária; π, a constante matemática fundamental; 1, o elemento básico da aritmética; e 0, o símbolo da inexistência. A beleza desta equação reside na maneira como une esses elementos aparentemente desconexos em uma expressão concisa e elegante.
Teorema de Pitágoras: A simplicidade por trás da complexidade
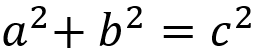
Outra equação que evoca admiração é o Teorema de Pitágoras. Esta simples expressão descreve a relação entre os comprimentos dos lados de um triângulo retângulo. Apesar de sua simplicidade aparente, o Teorema de Pitágoras é uma das descobertas matemáticas mais fundamentais e amplamente aplicáveis, servindo como base para inúmeras outras teorias e aplicações práticas.
Equação de Maxwell: A unificação da eletricidade e do magnetismo
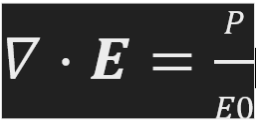
Um exemplo marcante de beleza matemática na física é a Equação de Maxwell. Esta equação descreve como as cargas elétricas geram campos elétricos, representando uma das quatro equações fundamentais do eletromagnetismo. A elegância da Equação de Maxwell reside em sua capacidade de unificar os fenômenos elétricos e magnéticos em um conjunto coeso de leis, revelando a profunda interconexão entre esses dois aspectos da natureza.
Equação de Schroedinger: A dança dos elétrons
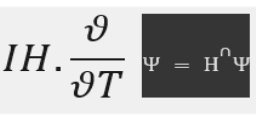
Na mecânica quântica, a Equação de Schroedinger desempenha um papel central, descrevendo o comportamento dos sistemas quânticos, como átomos e moléculas. Esta equação fundamental, descreve a evolução temporal da função de onda de um sistema quântico. Apesar de sua complexidade matemática, a Equação de Schroedinger encapsula a essência da estranha e fascinante natureza do mundo quântico.
Conclusão
As equações matemáticas, embora muitas vezes percebidas como meras ferramentas de cálculo, possuem uma beleza intrínseca que transcende sua utilidade prática. Da identidade de Euler à Equação de Schroedinger, essas expressões matemáticas oferecem uma janela para a ordem e a harmonia subjacentes ao universo. Ao explorar essas equações, somos lembrados da profunda conexão entre a matemática e a natureza, e da capacidade da mente humana de capturar e compreender a beleza abstrata que permeia o cosmos.
Curiosidade do dia: A matemática durante a Revolução Industrial
- Durante a Revolução Industrial, a matemática desempenhou um papel crucial na transformação da sociedade e na aceleração do progresso tecnológico. O desenvolvimento da matemática aplicada e da estatística foi fundamental para avanços em áreas como engenharia, economia e ciências físicas.
- Os avanços na matemática durante esse período foram impulsionados pela necessidade de resolver problemas práticos enfrentados pela indústria emergente. A geometria analítica de Descartes e o cálculo de Newton e Leibniz foram aplicados no projeto de máquinas e na análise de processos industriais.
- Além disso, a estatística começou a ser usada para análise de dados industriais, permitindo o controle de qualidade e a otimização de processos de produção. O trabalho pioneiro de Francis Galton e Karl Pearson na teoria estatística foi fundamental para o desenvolvimento da ciência dos dados.
Desafio do dia: Problemas de otimização inspirados na história
1 – Durante a Revolução Industrial, um empresário chamado John está procurando otimizar a produção de sua fábrica de tecidos. Ele descobriu que, para cada metro de tecido produzido, ele gasta $10 em matéria-prima e $5 em custos de mão de obra. Ele pode vender cada metro de tecido por $30. No entanto, ele também precisa considerar o custo fixo mensal da fábrica, que é de $500.
Para maximizar o lucro mensal da fábrica, John precisa determinar quantos metros de tecido deve produzir por mês. Qual é a quantidade ideal de metros de tecido que John deve produzir para maximizar seu lucro?





0 Comentários