Equação do Segundo Grau: Uma Janela para o Mundo das Incógnitas

Introdução:
No vasto campo da matemática, um dos tópicos mais abordados e importantes é a resolução de equações, onde os estudantes são introduzidos a equações do segundo grau, também conhecidas como equações quadráticas. Este tópico é fundamental para o desenvolvimento das habilidades matemáticas, pois permite aos alunos explorar uma classe especial de equações com um papel crucial em várias áreas da matemática e ciências, bem como em aplicações do mundo real. Este conteúdo tem como objetivo explorar a equação do segundo grau, suas características, métodos de resolução e aplicações, proporcionando uma compreensão mais profunda deste conceito matemático essencial.
O que é uma equação do segundo grau?
Uma equação do segundo grau é uma expressão matemática que envolve uma incógnita elevada ao quadrado, ou seja, uma variável desconhecida representada por “x” está elevada ao expoente 2. A forma geral de uma equação do segundo grau é:
ax2+bx+c=0
Onde “a”, “b” e “c” são coeficientes constantes, e “a” não pode ser igual a zero, pois a equação perderia seu caráter de segundo grau. Os valores de “x” que tornam a equação verdadeira são chamados de raízes ou soluções da equação.
- Métodos de Resolução
Existem vários métodos para resolver equações do segundo grau, sendo os mais comuns:
- Fatoração: Este método envolve a fatoração da expressão do segundo grau em dois binômios e, em seguida, a igualação de cada binômio a zero. Por exemplo, considere a equação: x2−5x+6=0. Fatorando, obtemos (x−2).(x−3)=0. Igualando cada binômio a zero, encontramos as soluções: x=2 e x=3.
- Fórmula Quadrática: A fórmula quadrática é uma fórmula geral que permite encontrar as raízes de qualquer equação do segundo grau. É dada por:
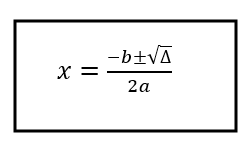
Onde “a”, “b” e “c” são os coeficientes da equação. Por exemplo, para resolver a equação 2x2−3x−5=0, podemos usar a fórmula quadrática para encontrar as soluções.
- Completando o Quadrado: Este método envolve transformar a equação do segundo grau em uma forma quadrada perfeita e, em seguida, encontrar suas raízes. É útil quando a fatoração não é óbvia. Por exemplo, para resolver a equação x2+6x+9=0, podemos completar o quadrado e obter a solução: x=−3.
O discriminante (Δ) é uma parte fundamental da fórmula quadrática e é dado por:
Δ=b2−4ac
Ele desempenha um papel importante na determinação do tipo de soluções que uma equação do segundo grau possui:
- Se Δ>0, a equação possui duas raízes reais e distintas.
- Se Δ=0, a equação possui duas raízes reais e iguais.
- Se Δ<0, a equação não possui raízes reais, mas sim raízes complexas.
Por exemplo, para a equação x2−4x+4=0, o discriminante é Δ=0, o que significa que ela possui duas raízes reais e iguais.
- Aplicações das Equações do Segundo Grau
As equações do segundo grau têm uma ampla gama de aplicações na vida cotidiana e em diversas áreas da matemática e ciências. Alguns exemplos de aplicação incluem:
- Física: Equações do segundo grau são frequentemente usadas para descrever o movimento de objetos em queda livre, o lançamento de projéteis e o comportamento de sistemas mecânicos.
- Economia: Equações quadráticas são usadas em análises financeiras para modelar o crescimento de investimentos, preços de produtos e receitas de empresas.
- Engenharia: Engenheiros usam equações do segundo grau para projetar estruturas, sistemas elétricos e sistemas de controle.
- Ciências Naturais: Em química, as equações quadráticas são usadas para resolver problemas relacionados a concentrações de substâncias e reações químicas.
- Computação: Algoritmos e métodos de resolução de equações do segundo grau são amplamente utilizados em programação e análise de dados.
Conclusão
As equações do segundo grau desempenham um papel crucial na matemática e em muitas áreas da vida cotidiana. Elas representam um ponto de entrada importante para o estudo de equações mais complexas e sistemas de equações. Portanto, compreender e dominar este tópico é essencial para o desenvolvimento acadêmico e profissional, permitindo aos indivíduos abordar uma variedade de problemas de forma mais eficaz e precisa.
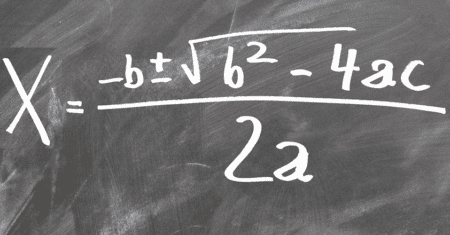

0 Comentários