Equação do 2º grau

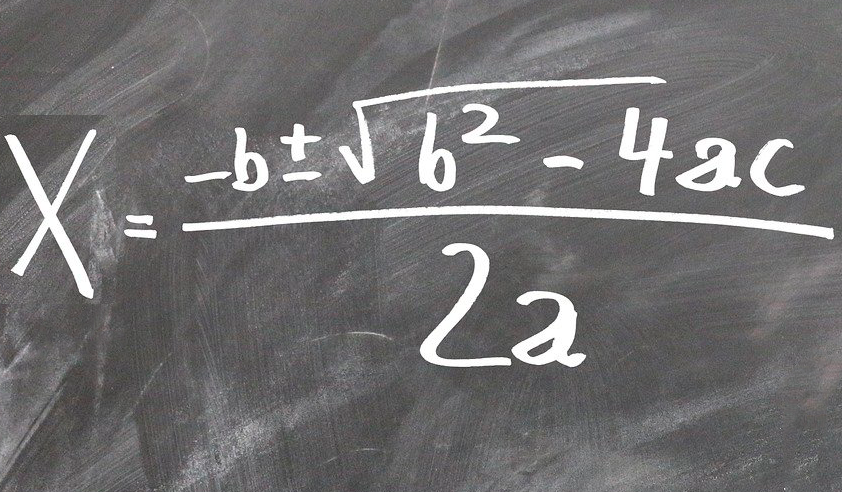
Teoria

Problemas com equações do 2º grau vem de mais de 2 mil anos atrás. Uma evidência disto é o Papiru de Rhind, onde os egípcios já tinham uma noção de como se resolviam problemas que envolviam equações do 2º grau.

Forma geral de uma equação do 2º grau

ax^2+bx+c=0

Para ser uma equação do 2º grau precisamos que a,\ b\ e\ c\ \in\ \mathbb{R},\ onde\ a\ \neq0 , em outras palavras, a,\ b\ e\ c\ pertencem ao conjunto dos Números Reais e a\ precisa ser um número diferente de zero (ou seja, um número positivo ou negativo).

a,\ b\ e\ c\ são chamados de coeficientes e são eles que determinam se uma equação do 2º grau é completa ou incompleta.

Equação do 2º grau completa e incompleta

Uma equação do 2º grau só é completa quando todos os coeficientes a,\ b\ e\ c\ são números (positivos ou negativos). Por definição a\ nunca poderá ser zero, logo para que a equação do segundo grau seja incompleta basta que b\ ou c\ seja zero.

Exemplo de equações completas:

• 2x^2+5x-1=0 , onde a=2, b=5, c=-1
• -x^2+x-3=0 , onde a=-1, b=1, c=-3
• x^2+2x+2=0 , onde a=1, b=2, c=2

Exemplo de equações incompletas:

• 2x^2+5x=0 , onde a = 2, b = 5, c=0
• -x^2-1=0 , onde a=-1, b=0, c=-1
• x^2=0 , onde a=1, b=0, c=0

Os coeficientes são de suma importância para solução da equação de segundo grau, precisamos deles para fazer a tão temida Fórmula de Bháskara:

x=\ \frac{-b\pm\sqrt{b^2-4ac}}{2a}

Mas antes de sairmos fazendo um monte de contas, vamos analisar a fórmula e ver que ela nos ajuda a ter informações importantes sobre as suas soluções. Para facilitar as contas utiliza-se a letra grega delta ( \Delta ) no lugar de b^2-4ac , pois como a expressão está dentro de uma raíz quadrada então sabemos que:

• Raízes quadradas em seu interior não admitem números menores que zero (números negativos), pois não existem soluções dessas raízes quadradas com números negativos nos Números Reais.
• Caso b^2-4ac seja igual a zero, independente do que colocarmos na fórmula de Bháskara obteremos sempre apenas uma resposta.
• Caso b^2-4ac seja maior que zero (número positivo) sempre teremos duas soluções que são distintas.

Dito isto, temos que \Delta=b^2-4ac , logo:

• \Delta<0 , se o resultado de delta for um número negativo, não há soluções.
• \Delta=0 , se o resultado de delta for zero, há apenas uma solução.
• \Delta>0 , se o resultado de delta for um número positivo, há duas soluções diferentes.

As soluções das equações do segundo grau são chamadas de raízes.

Tags: Álgebra | EF09MA09 | Equação do 2º grau | Fórmula de Bhaskara