Demonstração da Fórmula de Bhaskara
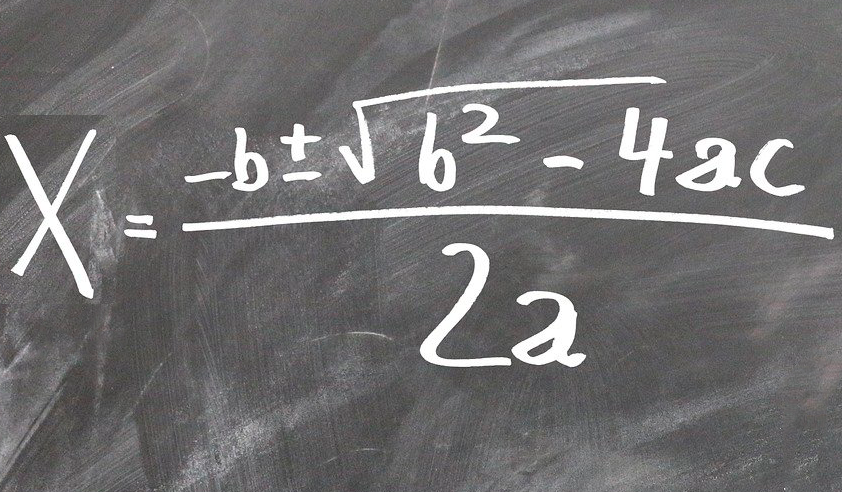
A demonstração da Fórmula de Bhaskara é um pouco complicada, mas nada impossível, preste atenção a cada detalhe da demonstração.
Para a demonstração, vamos começar com a forma geral de uma equação do 2º grau.
ax^2+bx+c=0Para o início da brincadeira iremos multiplicar os dois membros da equação por \frac{1}{a} , então fica da seguinte forma:
\frac{ax^2}{a}+\frac{bx}{a}+\frac{c}{a}=\frac{0}{a}Realizando as demais operações chegamos até a equação:
x^2+\frac{b}{a}x=-\frac{c}{a}Agora iremos somar \frac{b^2}{4a^2} aos dois membros da equação, a fim de formar no membro esquerdo da equação um trinômio quadrado perfeito.
x^2+\frac{b}{a}x\ +\frac{b^2}{4a^2}=-\frac{c}{a}+\frac{b^2}{4a^2}Portanto, realizaremos as seguintes simplificações:
\left(x+\frac{b}{2a}\right)^2=\ \frac{-4ac+b^2}{4a^2} \left(x+\frac{b}{2a}\right)^2=\ \frac{b^2-4ac}{4a^2}Como temos um dos membros da equação elevado ao quadrado iremos fazer a raiz quadrada dos dois membros da equação:
\sqrt{\left(x+\frac{b}{2a}\right)^2}=\ \sqrt{\frac{b^2-4ac}{4a^2}}Aplicando as simplificações pertinentes obtemos:
x+\frac{b}{2a}=\ \frac{\sqrt{b^2-4ac}}{\sqrt{4a^2}}Note que \sqrt{4a^2} possui duas soluções: +2a ou -2a , por isso aparece o mais ou menos na fórmula:
x+\frac{b}{2a}=\pm\ \frac{\sqrt{b^2-4ac}}{2a}Por fim, realizando as operações obtemos a fórmula de Bhaskara:
x=-\frac{b}{2a}\pm\ \frac{\sqrt{b^2-4ac}}{2a} x=\ \frac{-b\pm\sqrt{b^2-4ac}}{2a}OBSERVAÇÃO: Para facilitarmos as contas utilizamos na fórmula a letra grega delta ( \Delta ), onde:
\Delta=b^2-4acPortanto, a fórmula de Bhaskara mais difundida é:
x=\ \frac{-b\pm\sqrt\Delta}{2a}Espero que a demonstração da Fórmula de Bhaskara te ajude em seus estudos!
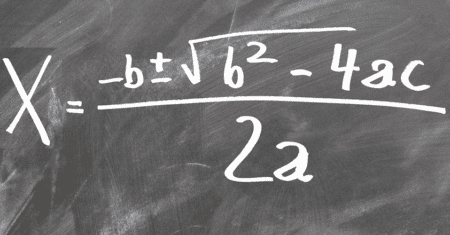



0 Comentários