Categoria: Teorema do dia

A Matemática na Previsão do Tempo: Desvendando os Mistérios Atmosféricos
Leitura: 3 min
Em suma, a previsão do tempo é um campo multidisciplinar que depende fortemente da matemática para entender e prever os complexos fenômenos atmosféricos. Desde a modelagem matemática até a coleta e processamento de dados, a matemática desempenha um papel fundamental em todos os aspectos do processo de previsão. Com o avanço da tecnologia e das técnicas de modelagem, as previsões do tempo continuam a melhorar, proporcionando informações valiosas para a sociedade.

Teorema do dia: A “natureza” matemática
Leitura: 3 min
A natureza tem sido uma fonte inesgotável de inspiração para a matemática ao longo dos séculos. Os padrões, formas e fenômenos observados na natureza frequentemente levam a descobertas matemáticas profundas e teoremas importantes. A Sequência de Fibonacci e a Proporção Áurea, o Teorema da Bola de Neve de Kepler e os fractais são apenas alguns exemplos de como a observação cuidadosa da natureza pode levar a avanços significativos na compreensão matemática do mundo ao nosso redor.
Teorema: O princípio de inclusão – exclusão
Leitura: 4 min
O princípio de inclusão-exclusão é uma ferramenta poderosa na contagem de elementos de conjuntos intersecionados. Sua aplicação é vasta, estendendo-se desde a matemática discreta até a probabilidade. Compreender e dominar este teorema é fundamental para resolver uma variedade de problemas em diferentes áreas da matemática e além. Ao aplicar esse princípio, podemos abordar questões complexas de forma sistemática e precisa, tornando-o uma peça central na caixa de ferramentas de todo matemático e cientista.

Teorema: O paradoxo de Banach-Tarski.
Leitura: 4 min
Em conclusão, o paradoxo de Banach-Tarski desafia nossa compreensão intuitiva de como o volume e a divisibilidade funcionam em espaços tridimensionais infinitos. Embora inicialmente desconcertante, ele é um resultado legítimo da teoria dos conjuntos e demonstra como conceitos aparentemente simples podem ter implicações profundas e não intuitivas. Esse paradoxo também destaca a importância da precisão conceitual e do rigor na formulação e compreensão de teorias matemáticas, mesmo quando essas teorias desafiam nossa intuição mais básica.

Teorema: Introdução a Teoria dos Números
Leitura: 4 min
Em conclusão, o Teorema Fundamental da Aritmética é uma pedra angular na teoria dos números, proporcionando uma compreensão profunda da estrutura dos números inteiros. A unicidade da decomposição em fatores primos, estabelecida por esse teorema, tem implicações significativas em várias áreas da matemática e da computação. Os números primos, com sua natureza enigmática e padrões intrigantes, continuam a desafiar e fascinar matemáticos e cientistas da computação em todo o mundo.

Teorema: A teoria dos grafos e suas aplicações
Leitura: 4 min
A teoria dos grafos é um campo fundamental da matemática discreta com uma ampla gama de aplicações práticas em diversas áreas. O Teorema das Cores de Vértices, um dos principais resultados dessa teoria, tem aplicações significativas em redes sociais, logística, circuitos eletrônicos e jogos. Ao compreender e aplicar os princípios da teoria dos grafos, é possível resolver problemas complexos de forma eficiente e encontrar soluções inovadoras em diferentes contextos. Portanto, o estudo e a aplicação dessa teoria continuam a desempenhar um papel crucial no avanço de várias áreas do conhecimento e da tecnologia.

Teorema do dia: Introdução ao Cálculo Integral
Leitura: 4 min
Em resumo, o Teorema Fundamental do Cálculo Integral é uma ferramenta poderosa que estabelece uma relação profunda entre diferenciação e integração. Sua compreensão é essencial para resolver uma variedade de problemas em matemática e disciplinas relacionadas. Ao compreender os componentes-chave deste teorema e sua aplicação em contextos práticos, os estudantes e profissionais podem expandir seu domínio sobre o cálculo e suas aplicações em diversas áreas do conhecimento.

Teorema de Euler
Leitura: 3 min
O Teorema de Euler para poliedros é uma contribuição significativa para a teoria dos poliedros e tem vastas aplicações em diferentes campos da matemática e da engenharia. Ao longo deste texto, exploramos o teorema, apresentando sua formulação, exemplos ilustrativos e implicações práticas. Ele continua a ser uma ferramenta indispensável para os matemáticos e cientistas, destacando a elegância e a profundidade que podem ser encontradas na teoria matemática.

Teorema: Princípio da Casa dos Pombos
Leitura: 4 min
Em resumo, o Teorema do Princípio da Casa dos Pombos é uma ferramenta versátil e indispensável em diversas áreas da matemática e ciências correlatas. Sua aplicação não se limita à mera contagem de elementos, mas se estende à análise de algoritmos, ciências da computação e muitos outros campos. Sua elegância reside na simplicidade de sua formulação e na amplitude de suas aplicações. Ao reconhecer a inevitabilidade de certas situações em sistemas de distribuição, o Princípio da Casa dos Pombos fornece uma base sólida para a resolução de problemas complexos. Assim, permanece como uma ferramenta indispensável no arsenal matemático para lidar com uma ampla gama de desafios analíticos e de contagem.
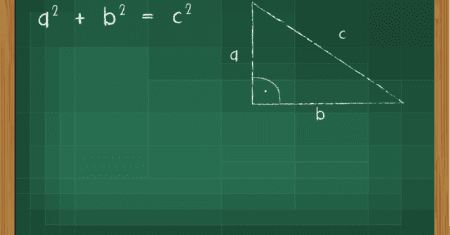
Teorema de Pitágoras: Precursor da Geometria
Leitura: 2 min
O Teorema de Pitágoras, ferramenta matemática poderosa e versátil, apresenta uma gama de aplicações práticas em diversas áreas, desde a construção civil até a astronomia e a navegação.