Explorando Funções Lineares

Introdução:
A matemática desempenha um papel fundamental no currículo escolar, e o estudo das funções é uma parte essencial desse campo. No ensino médio, os alunos são introduzidos a vários tipos de funções, incluindo as funções lineares. As funções lineares são particularmente importantes, pois representam um dos conceitos matemáticos básicos que têm aplicações em diversas áreas da vida cotidiana, desde a economia até a física. Neste texto, exploraremos o conteúdo das funções lineares de forma detalhada, apresentando conceitos, propriedades e exemplos práticos.
O que é uma Função Linear?
https://mundodamatematica.com.br/rascunho-automatico-funcao/
Uma função linear é um tipo específico de função matemática cuja representação gráfica forma uma linha reta. Ela é definida pela forma geral da equação:
f(x)=ax+b
Onde:
- f(x) é o valor da função dependente.
- x é o valor da variável independente.
- a é o coeficiente angular, que determina a inclinação da reta.
- b é o coeficiente linear, que determina o ponto onde a reta intercepta o eixo vertical.
Propriedades das Funções Lineares:
- Inclinação Constante: A característica distintiva das funções lineares é que a inclinação da reta (representada por a) é constante em todo o seu domínio. Isso significa que a taxa de mudança da função é a mesma para todos os valores de x.
- Intercepto Vertical: O valor de b determina onde a reta corta o eixo vertical. Esse ponto é chamado de intercepto vertical.
- Domínio e Contradomínio: O domínio de uma função linear é todo o conjunto dos números reais, enquanto o contradomínio também consiste nos números reais.
Exemplos de Funções Lineares:
- Exemplo 1: Modelagem de Custo
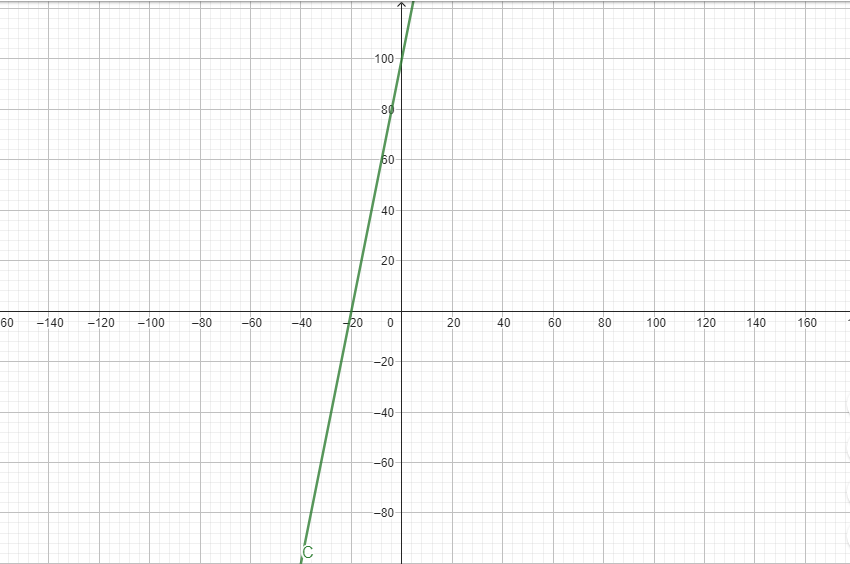
Suponhamos que uma empresa de produção de camisetas tenha um custo fixo de $100 e um custo variável de $5 por camiseta produzida. A função que descreve o custo total C(x) em relação ao número de camisetas produzidas x é dada por:
C(x)=5x+100
Neste caso, 5 é o coeficiente angular, representando o custo variável por camiseta e 100, é o coeficiente linear, representando o custo fixo.
- Exemplo 2: Representação Gráfica
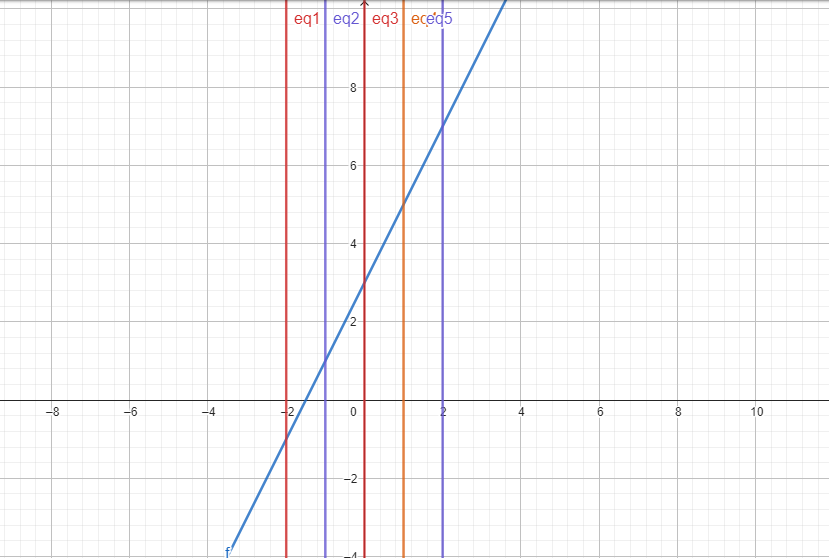
A representação gráfica de uma função linear é uma linha reta no plano cartesiano. Considere a função f(x)=2x+3. Se plotarmos os pontos para alguns valores de x, como -2, -1, 0, 1, e 2, obteremos uma linha reta com inclinação 2 e intercepto vertical 3.
Conclusão:
As funções lineares são amplamente utilizadas em diversas áreas, desde a economia até a física, para modelar relacionamentos simples e prever resultados. Ao compreender os conceitos das funções lineares, os alunos estarão preparados para explorar tópicos mais complexos no futuro e aplicar seus conhecimentos em situações do mundo real. Portanto, aprofundar o estudo das funções lineares é uma parte crucial do desenvolvimento matemático.




0 Comentários